زاویه (ریاضیات)
زاویه (ریاضیات)(angle)
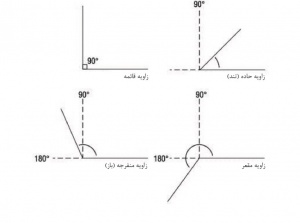
در ریاضیات، مقدار چرخش یا دَوَران[۱]. آن را با دو پرتو (نیمخط[۲]) با مبدأ مشترک که بر یک خط واقع نیستند، مشخص میکنند. بهشکل حاصل نیز زاویه میگویند. مبدأ مشترک را رأس[۳] و دو پرتو را ضلعهای[۴] زاویه مینامند. زاویه را با درجه[۵] ( ْ) یا رادیان[۶] (rad) یا گراد اندازهگیری میکنند. یک دور چرخش کامل یا دایره[۷] ْ۳۶۰ یا ۲π رادیان یا ۴۰۰ گراد است. زاویهها را معمولاً بنا به اندازهشان برحسب درجه طبقهبندی میکنند. زاویۀ حاده[۸] (تند) کوچکتر از ْ۹۰ و زاویۀ قائمه (راست) دقیقاً برابر ْ۹۰ یا یک ربع دایره است. دو زاویه را که مجموعشان ْ۹۰ باشد، زوایای متمم[۹] مینامند. زاویۀ منفرجه[۱۰] (باز) بزرگتر از ْ۹۰، ولی کوچکتر از ْ۱۸۰ (زاویۀ نیمصفحه[۱۱] یا دو قائمه) است. زاویۀ محدب[۱۲] بین ْ۰ و ْ۱۸۰ و زاویۀ مقعر[۱۳] بزرگتر از ْ۱۸۰ ولی کوچکتر از ْ۳۶۰ اند. دو زاویه را که مجموعشان ۱۸۰ باشد، زوایای مکمل[۱۴] مینامند. زاویهای که رأس آن روی محیط دایره و یکی از ضلعهای آن وتری[۱۵] از دایره و ضلع دیگرش خط مماس بر دایره در رأس باشد، زاویۀ ظلی[۱۶] خوانده میشود. اندازۀ زاویۀ ظلی نصف اندازۀ کمان روبهروی آن است. زاویۀ مرکزی زاویهای است که رأس آن در مرکز دایره و ضلعهایش شعاعهای دایرهاند. اندازۀ زاویۀ مرکزی برابر با اندازۀ کمان روبهروی آن است.
زاویۀ دووجهی. شکل حادث از یک خط و دو نیمصفحه[۱۷] است، به قسمی که خط، فصل مشترک آنها باشد. این خط را یال[۱۸] زاویۀ دووجهی[۱۹]، و اجتماع خط و هر یک از دو نیمصفحه را وجه[۲۰] مینامند. زاویۀ دووجهی را با زاویۀ مسطحه[۲۱]اش اندازهگیری میکنند. برای رسم این زاویه، از نقطهای روی یال دو خط عمود بر یال رسم میشود که هر یک در یکی از دو صفحه قرار دارند.
زاویۀ چندوجهی یا کنج[۲۲]. شکل حادث از تقاطع حداقل سه وجه یک چندوجهی است که در رأس مشترکاند.
زاویۀ خط با منحنی. زاویهای است که خط در نقطۀ تقاطع با منحنی، با خط مماس[۲۳] بر منحنی در آن نقطه میسازد.
زاویۀ دو منحنی. زاویۀ بین مماسهای دو منحنی در نقطۀ تقاطع آنهاست.
زاویه در مثلث. زاویههای حاصل از تقاطع دوبهدوی اضلاع مثلث در درون مثلث زاویههای داخلی[۲۴]اند. مثلث دارای سه زاویۀ داخلی با مجموع ْ۱۸۰ است. هریک از زاویههای داخلی مثلث متساویالاضلاع[۲۵] ْ۶۰ است. زاویۀ خارجی[۲۶] در هر رأس زاویهای بین یک ضلع منتهی به آن رأس و امتداد ضلع دیگر منتهی به آن است. بنابراین، در هر رأس دو زاویۀ خارجی وجود دارد. اندازۀ هر زاویۀ خارجی برابر مجموع اندازههای دو زاویۀ داخلی غیرمجاور آن است. در مثلث قائمالزاویه[۲۷]، زوایای مجهول را با بهکاربردن مثلثات[۲۸] بهدست میآورند.
زاویه در چندضلعی. تعریف زاویههای داخلی و خارجی چندضلعی مانند تعریف زوایای مثلث است. زاویۀ مرکزی چندضلعی زاویهای است که رأس آن در مرکز چندضلعی قرار دارد و اضلاع آن دو پارهخطاند که از مرکز به دو سر یک ضلع وصل میشوند. در چندضلعی منتظم[۲۹]، زاویههای داخلی باهم برابر و زاویۀ مرکزی برابر با زاویۀ خارجی است و از تقسیم ْ۳۶۰ بر تعداد اضلاع چندضلعی بهدست میآید. مثلاً اندارۀ زاویۀ مرکزی ۸ضلعی ْ۴۵=۸÷ ْ۳۶۰ است.
زاویه در دایره. زاویهای که رأس آن روی محیط دایره قرار داشته باشد و ضلعهای آن وترهایی از دایره باشند، زاویۀ محاطی[۳۰] نامیده میشود. اندازۀ زاویۀ محاطی نصف اندازۀ کمان روبهروی آن است.
زاویههای متقابل به رأس. زاويههاي متقابل به رأس[۳۱] دو زاویهاند که رأس آنها مشترک، و ضلعِ هر یک از آنها در امتداد ضلع زاویۀ دیگر است.
- ↑ rotation
- ↑ half-line
- ↑ vertex
- ↑ sides
- ↑ degree
- ↑ radian
- ↑ circle
- ↑ acute angle
- ↑ complementary angles
- ↑ obtuse angle
- ↑ straight angle
- ↑ salient angle
- ↑ reflex angle
- ↑ supplmentary angles
- ↑ chord
- ↑ angles chord angle formed by a tangent and a chord
- ↑ straight
- ↑ edge
- ↑ dihedron
- ↑ face
- ↑ plane angle
- ↑ polyhedral angle
- ↑ tangent
- ↑ interior angles
- ↑ equilateral triangle
- ↑ exterior angle
- ↑ right-angled triangle
- ↑ trigonometry
- ↑ regular polygon
- ↑ inscribed angle
- ↑ vertical angles
