لیندمان، فردیناند فون (۱۸۵۲-۱۹۳۹)
لینْدِمان، فِردینانْد فون (۱۸۵۲-۱۹۳۹)(Lindemann, Ferdinand von)
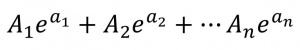

ریاضیدان آلمانی. کشف او در زمینۀ ماهیت[۱] عدد π در ۱۸۸۲ حل مسئلۀ قدیمی تربیع دایره[۲] را منتفی کرد. در هانوور[۳] زاده شد و در گوتینگن[۴]، مونیخ، و ارلانگن[۵] درس خواند. از ۱۸۷۹ تا ۱۸۸۳، در وورتسبورگ[۶] و از ۱۸۸۳ تا ۱۸۹۳، در کونیگسبرگ[۷] استاد بود. از ۱۸۹۳ تا آخر عمرش در مونیخ تدریس میکرد. این پرسش که عدد π متعالی[۸] (غیرجبری[۹]) است یا نه هرگز پاسخ قانعکنندهای نیافته بود تا اینکه لیندمان در ۱۸۸۲، متعالیبودن آن را در مقالهای ثابت کرد. او نشانداد که جز در حالات بدیهی، هر عبارت بهصورت (فرمول ۱) که در آن Aiها و ai ها عددهایی جبری باشند، غیرصفر است.
فرمول ۱:
بنابراین، چون i ریشۀ معادلۀ x۲ + ۱ = ۰ ، و معلوم است که eiπ + e- = ۰، یعنی eiπ = -۱؛ بنابراین لازم است π متعالی باشد، زیرا i جبری است. اگر π ریشۀ معادلهای جبری نباشد، ترسیمپذیر نیست و نمیتوان با خطکش غیرمدرج و پرگار، پارهخطی رسم کرد که طولش برابر آن باشد. به این ترتیب، تربیع دایره غیرممکن است.
