جایگشت
جایْگَشْت (permutation)
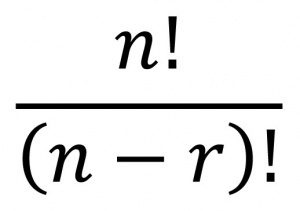

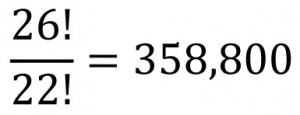

در ریاضیات متمایز، آرایش[۱] یا رشتۀ مرتبی از همۀ عضوهای دستهای از اشیاء یا تعدادی از آنها. تعداد جایگشتهای ممکنn شیء متمایز، اگر همۀ آنها در هر جایگشت بیایند، برابر است با !n ، که ! علامت فاکتوریل[۲] است. مثلاً جایگشتهای سه حرفی حروف z ,y ,x عبارتاند از zyx, zxy, yxz ,yzx ,xzy, xyz که تعداد آنها برابر است با ۶ = ۳ × ۲ × ۱ = !۳، اما تعداد جایگشتهای r شیء برگزیده از n شیء برابر است با (فرمول ۱).
فرمول ۱:
مثلاً اگر شش حرف متفاوت الفبا را در نظر بگیریم، تعداد جایگشتهای چهار حرف از میان این شش حرف برابر است با (فرمول ۲) با الفبایی که ۲۶ حرف دارد، تعداد کلمههای چهار حرفی ممکن، از لحاظ نظری، برابر است با (فرمول ۳).
فرمول ۲: فرمول ۳:
اگر بعضی اعضا در دستۀ n عضوی تکراری باشند، تعداد جایگشتها برابر است با !n تقسیم بر حاصلضرب فاکتوریلهای اعدادی که نشاندهندۀ تعداد دفعات تکرار اعضای تکراری هستند. مثلاً اگر شش حرف a,a,a,b,b,c را در نظر بگیریم، چون a سهبار و b دوبار تکرار شده است، تعداد جایگشتها برابر است با (فرمول ۴) نیز ← ترکیب
فرمول ۴:
