فیثاغورس (ح ۵۸۰ـ ۵۰۰پ م)
فیثاغورِس (ح ۵۸۰ـ ۵۰۰پم)(Pythagoras)
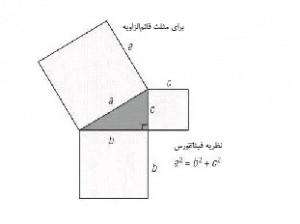
ریاضیدان و فیلسوف یونانی. قضیۀ فیثاغورس[۱] را عرضه کرد. بیشتر کارهای فیثاغورس دربارۀ اعداد است. او خصوصیات اسرارآمیزی به اعداد نسبت میداد. کشف اعداد مصور ازجمله کارهای او در این زمینه است؛ مثلاً اعداد مثلثی[۲] ...، ۱۰، ۶، ۳، ۱، که هریک را میتوان بهشکل آرایه[۳]ای مثلثشکل از نقاط نشان داد یا اعداد مربعی[۴] ...، ۱۶، ۹، ۴، ۱، که آرایههایی مربعی از نقاط تشکیل میدهند. همچنین، دریافت که مجموع دو عدد مثلثی متوالی عددی مربعی است، مثلاً ۴=۳+۱، ۹=۶+۳، و ۱۶=۱۰+۶. فیثاغورس در جزیرۀ ساموس[۵] زاده شد و ظاهراً از ظلم و جور حاکم خودکامۀ آنجا به کروتونه[۶] (کروتون) در ایتالیای جنوبی گریخت. در کروتون، مدرسهای تأسیس کرد که در ضمن نوعی جمعیت یا انجمن اخوت با شعائر و اعتقاداتی خاص، ازجمله اعتقاد به بقا و تناسخ، بود. انجمن ریاضی و فلسفی فیثاغورسی به توسعۀ علم پرداخت و از نظر سیاسی نیز دامنۀ نفوذ آن به مهاجرنشینهای غربی یونان رسید. این امر باعث کشمکش و اغتشاشی شد که به تبعید فیثاغورس به شهر متاپونتوم[۷]، در خلیج تارانتو[۸]، انجامید. فیثاغورس در این شهر درگذشت. مدرسۀ فیثاغورس حدود ۵۰ سال دایر بود و بعد از آن بهکلی ازهم پاشید. فیثاغورسیان، شاگردان و پیروان فیثاغورس، توانستند با استفاده از نظریۀ موازیها[۹] ثابت کنند که مجموع زاویههای هر مثلث معمولی برابر با دو زاویۀ قائمه[۱۰] است. همچنین، روشی برای حل هر معادلۀ درجۀ دوم جبری[۱۱] با ریشۀ حقیقی[۱۲] بهدست آوردند. آنها نظریۀ تناسبها (نسبتها)[۱۳] را تدوین کردند. این نظریه منجربه گسترش اطلاعات آنها دربارۀ کسرها[۱۴] شد و بهکمک آن، به مطالعۀ هارمونیکها (هماهنگها) در سازهای زهی پرداختند. آنها دریافتند که هارمونیک اوکتاو[۱۵] با لمسکردن تار در فاصلۀ یک دوم طول آن از یک انتها، هارمونیک پنجم در فاصلۀ دو سوم طول، و بقیه هارمونیکها نیز بههمین ترتیب ایجاد میشوند. کشف عدد گنگ[۱۶] را نیز به فیثاغورسیان نسبت دادهاند.
