تربیع دایره
تَربیعِ دایره (squaring the circle)
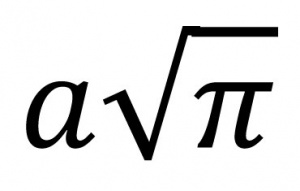
ترسیم مربعی که مساحتش برابر با مساحت یک دایره باشد. چنانچه در این ترسیم فقط استفاده از خطکش غیرمدرج و پرگار مجاز باشد، حل مسئله ممکن نیست، زیرا اگر شعاع چنین دایرهای a باشد، طول ضلع مربع، (فرمول ۱) عددی متعالی خواهد بود و رسم پارهخطی که طول آن عددی متعالی باشد، با استفاده از خطکش غیرمدرج و پرگار ممکن نیست.
فرمول ۱:
این مسئله یکی از سه مسئلۀ هندسی کلاسیک است که از دوران باستان مطرح بوده است و پس از آنکه فردیناند فون لیندمان[۱] در ۱۸۸۲ متعالیبودن عدد π را ثابت کرد، امتناع حل آن معلوم شد. نیز ← تضعیف_مکعب؛ تثلیث_زاویه
- ↑ Ferdinand von Lindemann
