مشتق
مُشتَق (derivative)
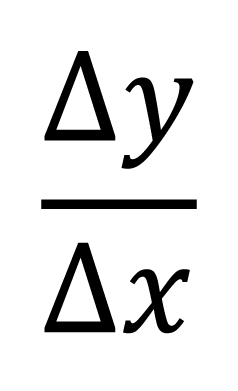
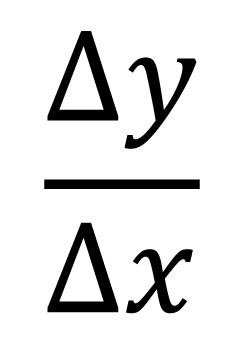
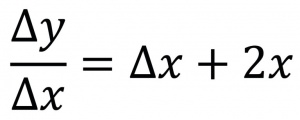
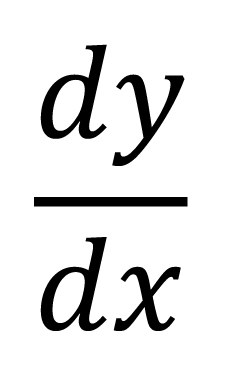
در ریاضیات، آهنگ[۱] یا نرخ دقیق تغییرات تابع[۲]، نسبت به تغییرات متغیر مستقل[۳]. در تابع یک متغیرۀ y =f (x)، اگر متغیر مستقل x به اندازۀ x∆، و تابع نیز متناظر با آن به اندازۀ ∆y = f (x+∆x) - f(x) تغییر کند، نسبت (فرمول ۱) آهنگ متوسط تغییر y به ازای تغییر x است.
فرمول ۱:
حال هرچه ∆x را کوچکتر بگیریم، یعنی تغییر تابع را بهازای تغییر کوچکتری از متغیر در نظر بگیریم، تصویر دقیقتری از نحوۀ تغییر تابع بهدست میآوریم. به این سبب، حدِ[۴] نسبتِ (فرمول ۲) را وقتی به صفر میل میکند، در صورتی که موجود و متناهی باشد، مشتق تابع f در x مینامند. مثلاً اگر y = x۲ و x به اندازۀ ∆x تغییر کند، y∆ یعنی تغییر متناظر y برابر ∆y = (x+∆x)۲- x۲ = ∆x۲+ ۲x∆x خواهـد بود. پس (فرمول ۳) آهنگ متوسط تغییر y نسبت به تغییر x است.
فرمول ۲: فرمول ۳:
حال اگر x∆ بهسمت صفر میل کند، ∆x + ۲x به ۲x میل میکند و بنابراین، مشتق این تابع ۲x است. در تعبیر هندسی، مشتق در نقطۀ x، شیب[۵] نمودار y = f (x) در نقطهای به طول x است؛ یعنی حد شیب خط قاطعی است که دو نقطه از این منحنی را بههم وصل میکند، وقتی که فاصلۀ این دو نقطه به صفر میل کند. مشتق تابع f در نقطۀ x، تابعی از x اسـت و آن را با f' (x) یا Df (x) یا (فرمول ۴) نشان میدهند.
فرمول ۴:
مشتق از اساسیترین مفاهیم حساب دیفرانسیل و انتگرال[۶] است و کاربردهای فراوان دارد، ازجمله برای تعیین شیب، صعودی یا نزولیبودن، یا تقعر نمودار تابع و یافتن ماکسیمم و مینیمم و بسیاری موارد دیگر بهکار میآید. این مفهوم برای توصیف پدیدههای طبیعی نیز در علوم دیگر کاربرد فراوان دارد، مثلاً، سرعت، مشتق مسافت نسبت به زمان، و شتاب، مشتق سرعت نسبت به زمان است.
