نمودار
نمودار (graph)
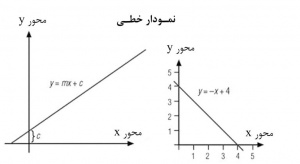
تصویری نشاندهندۀ رابطۀ دو یا چند متغیر[۱] ریاضی یا دستههایی از دادههای عددی[۲]، ازجمله دادههای آماری[۳]. برای رسم نموداری که رابطۀ دو متغیر را نمایش میدهد، معمولاً دو خط عمود برهم، به نام محور[۴]، رسم میکنند که نقطۀ تقاطع آنها مبدأ[۵] نام دارد. با درنظر گرفتن مبدأ بهمنزلۀ نقطۀ صفر، مقادیر دو متغیر، مثلاً مسافت و زمان برای شیء متحرک، را بهصورت نقاطی روی دو محور مشخص میکنند. سپس، برای نمایش هر جفت از مقادیر متناظر با دو متغیر، مثلاً مسافت معین و زمان صرفشده برای آن، عمودهایی بر دو محور رسم میکنند. نقطۀ تقاطع دو عمود نشاندهندۀ آن جفت از مقادیر است. آنگاه، این نقطهها را با منحنی همواری بههم وصل میکنند تا نمودار بهدست آید. معمولاً محور افقی را محور x و محور قائم را محور y مینامند. در این صورت، نمودار در دستگاه مختصات دکارتی[۶] رسم شده است. مختصات دکارتی هر نقطه مؤلفههاییاند که مکان نقطه را برحسب فاصلههای عمودی آن از دو یا چند محور یا خط مرجع[۷] تعیین میکنند. برای صفحه[۸]ای که با دو محور تعریف میشود، مختصات هر نقطه برحسب فواصل عمودی آن از محور y و محور x و بهصورت (x,y) بیان میشود. مثلاً نقطهای مانند p که به فاصلۀ سه واحد از محور y و چهار واحد از محور x قرار دارد، دارای مختصات (۴,۳) است. مختصات دکارتی را میتوان به ابعاد بالاتر نیز تعمیم داد. مثلاً در فضای سهبعدی، سه محور x و y و z وجود دارد و مختصات نقاط بهصورت سهتاییهای (x,y,z) اند. نمودار معادلۀ دومتغیره در صفحه، منحنیای شامل همۀ نقاطی است که مختصاتشان در آن معادله صدق میکنند و شامل نقطۀ دیگری نیست. خط راست نمودار معادلهای خطی[۹] بهشکل کلی y=mx+c است که m شیب خط، و c عرض از مبدأ[۱۰] یا مقدار y در نقطۀ تقاطع خط با محور y در دستگاه مختصات دکارتی است. نمودار معادلۀ دومتغیره در فضا استوانه، و نمودار معادلۀ سهمتغیره رویهای شامل همۀ نقاطی است که مختصاتشان در آن معادله صدق میکنند و شامل نقطۀ دیگری نیست. نمودار تابع f مجموعۀ همۀ نقاطی است که مختصاتشان جفتهای مرتب ((f (x و x)اند. گاهی نمودارهای ریاضی در مختصات قطبی[۱۱] رسم میشوند. سراشپون بافتنگار[۱۲] (بافتنما) نوعی نمودار است که در آمار برای نمایش فراوانی[۱۳] یا فراوانی نسبیِ[۱۴] دادهها بهکار میرود. برای رسم بافتنگار، پس از ردهبندی دادهها، ردهها را روی محور افقی و فراوانیها را روی محور قائم مشخص میکنند. سپس، مستطیلهایی روی ردهها ساخته میشود که مساحت آنها، و نه ارتفاع آنها بهصورتی که در نمودار میلهای بهکار میروند، متناسب با فراوانی ردههاست. بین مستطیلها فاصلهای گذاشته نمیشود. نمودار میلهای[۱۵] نوعی دیگر از نمودار است که معمولاً در آمار و برای نمایش فراوانیها بهکار میرود. این نمودار متشکل از تعدادی مستطیل موازی است که ارتفاع آنها متناسب با فراوانی دادههاست. این نمودار وقتی بهکار میرود که دادهها گسسته[۱۶] باشند.
