توپولوژی
توپولوژی (topology)
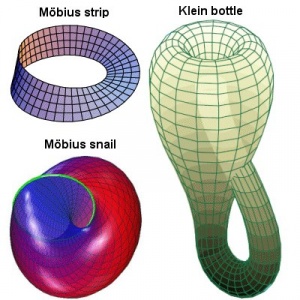

شاخهای از ریاضیات، برای بررسی ویژگیهایی از شکلهای هندسی که اگر شکل را با کشیدن، خمکردن، فشردن، و اعمالی از این قبیل به شکل دیگری تبدیل کنیم، آن ویژگیها تغییر نمیکنند. به بیان دقیقتر، علم بررسی ویژگیهایی که تحت تبدیل توپولوژیک[۱] یا همسانریختی[۲] ثابت میمانند. مثال ساده از مسائل توپولوژی نوار موبیوس است. اگر نواری را یک بار بپیچانیم و دو سرآن را به هم وصل کنیم، پشتوروی آنکه دو رویه دارد تبدیل به یک رویه میشود. تبدیل توپولوژیک تناظری دوسویی و در دو جهتپیوسته بین نقاط شکل اصلی و شکلِ تبدیلشده است. منظور از تناظر دوسویی[۳] این است که هر نقطه از شکل اصلی فقط با یک نقطه از شکل تبدیلشده متناظر است و بهعکس. منظور از پیوستگی در دو جهت این است که اگر دو نقطۀ دلخواه r و q از شکل اصلی و نقاط متناظر آنها 'r و 'q را از شکل تبدیلیافته درنظر بگیریم و r را تغییر مکان دهیم تا به q میل کند، 'r نیز به 'q میل خواهد کرد. اگر شکلی تحت تبدیل توپولوژیک به شکل دیگری تبدیل شود، آن دو شکل را همسانریخت[۴] مینامند و میگویند ویژگیهای توپولوژیک آنها یکی است یا از لحاظ توپولوژی با هم معادلاند. مثلاً اگر دایرهای از لاستیک را تصور کنیم و آن را بکشیم یا جمع کنیم بدون آنکه پاره شود یا دو نقطۀ آن روی هم بیفتد، میتوانیم آن را به شکلهای گوناگونی ازقبیل بیضی، مربع، و مثلث درآوریم. همۀ این شکلها با دایره همسانریختاند. اما اگر دایره را در نقطهای ببریم و آن را بکشیم تا بهصورت خط راست[۵] درآید، این تبدیل از نوع توپولوژیک نیست، زیرا دو سویی نیست و نقطۀ برش با دو نقطۀ انتهایی پارهخط[۶] متناظر میشود، حال آنکه هر نقطه از شکل اصلی باید فقط با یک نقطه از شکل تبدیلیافته متناظر شود. در مثال فوق، تبدیل پیوسته هم نیست. همچنین، میتوان کره را با این تبدیل بهصورت مکعب درآورد، امّا نمیتوان آن را بهصورت چنبرهای[۷] درآورد که در وسطش سوراخی باشد. تبدیل توپولوژیک ابعاد و زوایا را در حالت کلی تغییر میدهد، ولی بعضی از خواص را، که ویژگیهای توپولوژیکاند، ثابت نگه میدارد. موضوع علم توپولوژی بررسی این ویژگیها در شکلهای هندسی، و بهطور کلی مجموعههای نقاط است. مسئلۀ معروف به قضیۀ چهاررنگ، که در حوالی ۱۸۸۰ مطرح شد، نمونهای از مسائل توپولوژیک است. طبق این قضیه، برای رنگآمیزی نقشۀ جغرافیایی، بهطوری که هر دو کشورِ دارای مرز مشترک با رنگهای متمایز نشان داده شوند، چهار رنگ کافی است. این مسئله را پس از تلاشهای ناموفقِ بسیار، سرانجام کِنِت اَپِل[۸] و ولفگانگ هاکن[۹] در ۱۹۷۲ با رایانه حل کردند. نقشههای مترو و شبکۀ راهها که فقط نحوۀ اتصال راهها، و نه شکل و اندازۀ آنها را نشان میدهند، نمونهای از نمایش توپولوژیک شبکههاست. در حل مسئلۀ پل کونیگسبرگ[۱۰] هم، که اویلر[۱۱] در آن جزیرهها را با نقطه و پلها را با خط نشان داده، درواقع از نگرش توپولوژیک استفاده شده است. توپولوژی کاربردهای علمی مهمی، ازجمله در مطالعۀ تلاطم جریان سیالات، دارد. توپولوژی از رشتههای نسبتاً جدید ریاضیات است و عمدتاً در قرنهای ۱۹ و ۲۰ شکل گرفته است. ریشههای اولیۀ آن عبارتاند از تحقیق گئورک کانتور[۱۲] دربارۀ مجموعههای نقاط، تحقیق کارل وایرشتراس[۱۳] در زمینۀ مفهوم حد تابع، تحقیق کیرشهوف[۱۴] دربارۀ شبکههای برق، و استفادۀ برنهارد ریمان[۱۵] از اصول توپولوژی در تحقیقاتش راجع به رابطۀ سطوح و تابع. تکوین توپولوژی بهصورت شاخهای علمی عمدتاً در قرن ۲۰ و با تحقیقات هانری پوانکاره[۱۶] صورت گرفت.
