عدد
عدد (number)


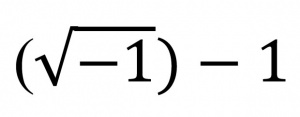

نمادی برای شمارش، اندازهگیری، مقایسۀ کمیتها، کدبندی اطلاعات، و محاسبات گوناگون. دستگاه اعداد[۱] متداول در زندگی روزمره و در اغلب مباحث علمی، دستگاه اعداد اعشاری[۲] یا دهدهی، در پایۀ[۳] ۱۰، است و در آن، هر عددی با یک یا چند رقم از ده رقمِ ۰، ۱، ۲، ۳، ۴، ۵، ۶، ۷، ۸، و ۹ نمایانده میشود. در رایانه، از دستگاه اعداد دودویی[۴]، در پایۀ ۲، استفاده میکنند که در آن دو رقم ۰ و ۱ بهکار میرود. در ریاضیات، انواع گوناگونی از اعداد وجود دارد. اعداد طبیعی[۵] همۀ عددهای ...,۱,۲,۳ هستند که برای شمارش بهکار میروند. اعداد صحیح[۶] عبارتانداز اعداد طبیعی و قرینههای آنها و صفر ...,۳ ±,۲ ±,۱ ±,۰ اعداد گویا[۷] کسرهای متعارفی[۸]اند، یعنی کسرهایی که صورت و مخرجشان اعدادی صحیحاند، با این شرط که مخرج صفر نباشد. بنابراین، اعداد صحیح را هم شامل میشوند. اعداد گنگ[۹] عددهاییاند که نمیتوان آنها را بهصورت کسر متعارفی نمایش داد و نشاندادن آنها با کسر اعشاری[۱۰] هم فقط به تقریب میسر است، زیرا سلسلۀ ارقامشان در نمایش اعشاری بیپایان و نامتناوب است. این اعداد شامل رقم یا سلسله ارقامی نیستند که دایم تکرار شوند. از اینرو، با رادیکال[۱۱]ها و نمادهای خاص دیگر نشان داده میشوند. مثلاً، اگر عددهای گنگ (فرمول ۱)، π ، و e را بهصورت اعشاری بیان کنیم به ترتیب و، با تقریب سه رقم اعشار برابرند با ۱.۴۱۴، ۳.۱۴۲، ۲.۷۱۸. اعداد π و e در عین حال نمونههایی از اعداد متعالی[۱۲] یا غیرجبری چسبیده است، یعنی اعدادی که، برخلاف (فرمول ۲)، ریشۀ معادلهای چندجملهای[۱۳] با یک کمیت متغیر[۱۴] یا مجهول و دارای ضرایب[۱۵] گویا نیستند.
فرمول ۱: فرمول ۲:
اعداد موهومی[۱۶] حاصلضرب ریشۀ دوم[۱۷] ۱- در اعداد حقیقیاند. اعداد مختلط[۱۸]، که هم اعداد حقیقی و هم اعداد موهومی را شامل میشوند، بهصورت a+bi اند که در آن، i ریشۀ دوم ۱- (فرمول ۳)، a قسمت حقیقی، وb قسمت موهومی عدد مختلطاند. اگر۰= b، این عدد حقیقی و اگر ۰= a، موهومیِ محض است.
فرمول ۳:
پیدایش دستگاههای اعداد. مصریان، یونانیان، رومیان، و بابلیهای باستان همه دستگاههایی از اعداد پدید آوردند، ولی هیچیک از این دستگاهها شامل صفر نبود. صفر، که ایجاد دستگاههای شمارِ مبتنیبر ارزش مکانی را امکانپذیر کرد، ابداع هندیان است و مسلمانان در قرن ۳ق آن را معرفی و ترویج کردند. صفر بعدها به اروپا راه یافت. دستگاه دهدهی یا اعشاری نیز براساس ارزش مکانی ارقام ساخته شده است. پس از آن، دستگاههای دیگری نیز بر این مبنا پدید آمده و کاربرد یافتهاند. از آن جمله است اعداد در پایۀ ۲ یا اعداد دودویی که در آنها، فقط از ارقام ۰ و ۱ استفاده میکنند و معمولاً در رایانههای رقمی و برای نشاندادن پالسهاس الکتریکیِ دوحالتیِ «روشن» یا «خاموش» بهکار میرود. اعداد دودویی را نخست گوتفرید لایبنیتس[۱۹] در قرن ۱۷ عرضه کرد.
تعریف انواع اعداد. مفاهیمی مانند عدد منفی، عدد گویا، و عدد گنگ را میتوان بهدقت برحسب اعداد طبیعی تعریف کرد. مسئلۀ مهم تعریف اعداد طبیعی است. در دوران اخیر، تعریف اعداد طبیعی و صفر بر حسب مجموعهها صورت می گیرد. صفر را بهصورت مجموعۀ تهی[۲۰] تعریف میکنند: ۰=Ø سپس، ۱ بهمنزلۀ اجتماع ۰ و مجموعهای مرکب از ۰، که یک عضو صفر دارد، تعریف میشود. به این ترتیب، میتوان ۲ را بهعنوان اجتماع ۱ و مجموعهای شامل ۱، که شامل دو عضو صفر و یک است، تعریف کرد و بههمین ترتیب ادامه داد. روش دیگر، تعریف اعداد حقیقی برحسب خصوصیات جبری و آنالیزی آنهاست.
- ↑ number system
- ↑ decimal system
- ↑ base
- ↑ binary number system
- ↑ natural numbers
- ↑ integers
- ↑ rational numbers
- ↑ common fractions
- ↑ irrational numbers
- ↑ decimal fraction
- ↑ radical
- ↑ transcendental numbers
- ↑ polynomial equation
- ↑ variable
- ↑ coefficients
- ↑ imaginary numbers
- ↑ second root
- ↑ complex numbers
- ↑ Gottfried Leibniz
- ↑ null set
