عدد فرما
عدد فِرْما (Fermat number)
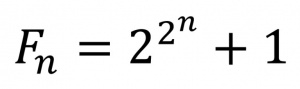
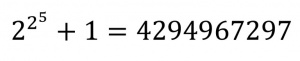
عددهای صحیحی[۱] به شکل (فرمول ۱)، به ازای n=۰, ۱, ۲, .... . فِرما، ریاضیدان فرانسوی، گمان میکرد همۀ آنها اعداد اول[۲]اند، زیرا ملاحظه کرده بود که F۰، F۱، F۲، F۳، F۴ اولاند. بعدها معلوم شد F۵، یعنی عدد (فرمول ۲) بر ۶۴۱ بخشپذیر است.
فرمول ۱: فرمول ۲:
عددهای فرمایی که اول هم باشند، اعداد اول فرما نامیده میشوند. تاکنون دانسته نیست عدد اول فرمایی بعد از F۴ وجود دارد یا نه، و نیز تعداد عددهای اول فرما نامتناهی[۳] است یا نه. بخشی از توجه به عددهای فرما ناشی از ارتباط آنها با مسئلۀ ترسیم چندضلعیهای منتظم[۴] با خطکش غیر مدرج و پرگار، بدون استفاده از وسائل دیگر، است. اگر n عدد اولی باشد، میتوان n ضلعی منتظمی را به این روش رسم کرد، به شرط آنکه n، عدد اول فرما باشد.
