مثلثات
مُثَلَّثات (trigonometry)

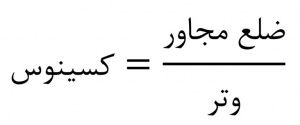



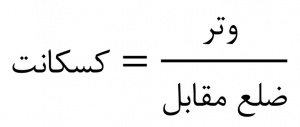

شاخهای از ریاضیات، بهمنظور محاسبۀ اجزای مثلثهای مسطحه[۱] و کروی[۲]، با استفاده از نسبتهای بین اضلاع مثلث قائمالزاویه[۳]، معروف به توابع مثلثاتی، بررسی ویژگیهای این توابع، و بهدستآوردن فرمولهای روابط بین آنها. متناظر با هر زاویۀ حاده[۴] در مثلث قائمالزاویه، شش نسبت اصلی بین ضلعها تعریف میشود که عبارتاند از سینوس[۵]، کسینوس[۶]، تانژانت[۷]، کتانژانت[۸]، سکانت[۹]، و کسکانت[۱۰]. این نسبتها در متون ریاضیات دورۀ اسلامی بهترتیب جیب، جیب تمام، ظل، ظل تمام، قطرظل، و قطر ظل تمام نامیده شدهاند. اگر اندازۀ یک زاویه و طول یک ضلع یا طول دو ضلع از مثلث قائمالزاویهای معلوم باشد، بقیۀ اجزای مثلث را میتوان با استفاده از مثلثات تعیین کرد. بلندترین ضلع مثلث قائمالزاویه که روبه زاویۀ قائمه است، وتر[۱۱] نام دارد. دو ضلع دیگر، برحسب موقعیتشان نسبت به زاویۀ موردنظر، نامگذاری میشوند، یعنی یکی ضلع مقابل به زاویه و دیگری ضلع مجاور به آن نامیده میشود. به این ترتیب، شش نسبت مثلثاتی چنیناند: (فرمول ۱، فرمول ۲، فرمول ۳، فرمول ۴، فرمول ۵، فرمول ۶) هریک از این نسبتها فقط تابع زاویه است.
فرمول ۱: فرمول ۲: فرمول ۳: فرمول ۴: فرمول ۵: فرمول ۶:
تعریف این توابع را میتوان به هر زاویهای تعمیم داد. مثلثات کروی به محاسبۀ اجزای مثلث کروی میپردازد، ولی فرمولهایی که در آن بهکار میرود با فرمولهای مثلثهای مسطحه یکسان نیست. مثلثات کاربردهای مهمی در نجوم، دریانوردی، مساحی، و فیزیک دارد. مثلثات از مطالعۀ نجوم نشأت گرفت و یکی از بنیانگذاران آن هیپارخوس[۱۲] (اَبرخُس)، منجم یونانی، بود. بطلمیوس[۱۳]، منجم دیگر یونانی، این موضوع را بسیار گسترش داد. سینوس را هندیان، تانژانت را حبش حاسب، و سکانت و کسکانت را ابوالوفای بوزجانی ابداع کردند. در ۱۴۶۷م، رگیومونتانوس[۱۴] هنگام تنظیم جدولهای خود، مثلثات را بهمنزلۀ علمی مستقل تعریف کرد.
