انتگرال گیری
اَنْتگرالگیری (integration)
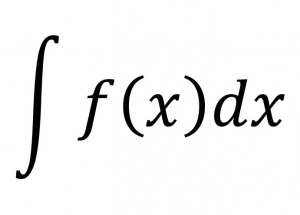
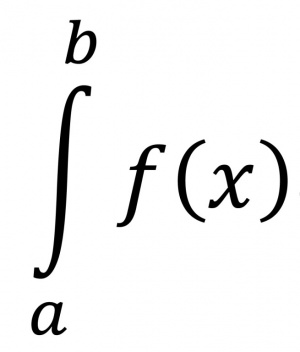
در ریاضیات، محاسبۀ انتگرال معین[۱] یا نامعین[۲]. منظور از انتگرال نامعین یک تابع[۳] مفروض هر تابعی است که مشتق آن، تابع مفروض باشد و به پادمشتق[۴] یا تابع اولیۀ[۵] تابع مفروض هم معروف است. اگر g انتگرال نامعینی از تابع f باشد، g + c هم که در آن c عدد ثابت دلخواه است، انتگرال نامعین f است. انتگرال نامعین تابع f را نسبت به x به صورت (فرمول ۱) نشان میدهند.
فرمول ۱:
تعیین سطح زیر منحنی بین دو مقدار خاص از متغیر یک تابع، که منحنی با آن تابع نمایش داده شده است، نمونهای از محاسبۀ انتگرال معین است. اگر این منـحنی نمودار تابع پیوسته[۶] و نامنفی (f (x بین دو مقدار a و b از متغیر x باشد، سطح زیر منحنی را با (فرمول ۲) نشان میدهند که برابر با (F(b)-F(a است و در این حالت، F پادمشتق یا انتگرال نامعین f است.
فرمول ۲:
اصول اساسی انتگرالگیری را در دهۀ ۱۶۶۰ فیلسوف آلمانی، لایبنیتس[۷]، و دانشمند انگلیسی، نیوتون، مستقل از هم کشف کردند.
