تکمیل مربع
تَکمیل مُرَبّع (completing the square)
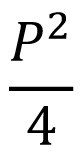
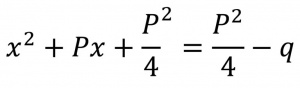
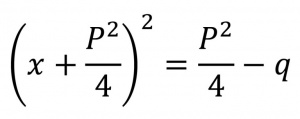
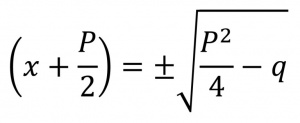
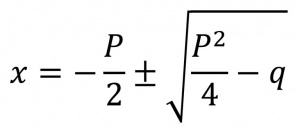
بهدستآوردن مربع کامل[۱] یا عبارتی به توان دو، از یک عبارت درجۀ دوم[۲]، با افزودن و کاستن ثابت مناسب. این عمل در اصل برای حل معادلۀ درجۀ دوم[۳] صورت میگرفته است. به این منظور، نخست همۀ جملههای معادله را بر ضریب جملۀ توان دو تقسیم میکنند و آنگاه همه را بهطرف چپ معادله میبرند تا معادله بهصورت x۲ + qx + q = ۰ درآید. سپس، مینویسد x۲ + qx = -q . بعداً (فرمول ۱) را به طرفین معادله اضافه میکنند: (فرمول ۲) یا (فرمول ۳).
طرف چپ معادله مربع کامل است و میتوان از آن ریشۀ دوم گرفت. پس، (فرمول ۴) و درنتیجه (فرمول ۵).
تکمیل مربع کاربردهای دیگری نیز دارد. ازجمله آنکه هنگام تحویل[۴] معادلات مقاطع مخروطی[۵] بهشکل متعارف، عبارتی بهشکل a۱x۲ + b۱x + c را بهشکل a۱ (x + b۲)۲ + c۲ درمیآورند.
تصاویر این فرمولها را در گوشه سمت چپ این مقاله آمده است:
