حد (ریاضیات)
حَدّ (ریاضیات)(limit)






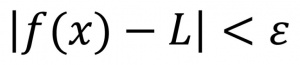


در دنبالۀ نامتناهی[۱]، مقدار ثابتی که دنباله درنهایت به آن میل میکند؛ بهعبارت دیگر، بهازای هر فاصلۀ دلخواه و هرقدر کوچک، فاصلۀ جملههای دنباله از آن مقدار ثابت، از جملهای بهبعد، از فاصلۀ موردنظر کمتر میشود. به زبان ریاضی، میگویند دنبالۀ {an} (...,۱,۲,۳=n)، وقتی n به بینهایت[۲] میل میکند، دارای حد L است، اگر بهازای هر عدد مثبت دادهشده مانند ε، هرقدر کوچک، عدد صحیح مثبتی مانندN وجود داشتهباشد، چنان که بهازای هرn >N (فرمول ۱) مثلاً حد دنبالۀ (فرمول ۲) صفر است، زیرا میتوان بهازای هر عدد مثبتی، هرقدر کوچک، N را چنان مشخص کرد که جملات بعد از جملۀ N ام، اختلافشان با صفر کمتر از آن عدد باشد.
فرمول ۱: فرمول ۲:
مثلاً، اگر عدد را یک میلیونیم در نظر بگیریم، ازجملۀ یک میلیونیم بهبعد، اختلاف جملهها با صفر کمتر از یک میلیونیم است. حد نسبتهای دنبالۀ فیبوناتچی[۳] برابر (فرمول ۳)، یعنی همان نسبت طلایی[۴]، است.
فرمول ۳:
حد تابع[۵] در یک نقطه، مقداری است که تابع بهاندازۀ دلخواه به آن نزدیک میشود، اگر متغیر[۶] را بهاندازۀ کافی نزدیک به آن نقطه در نظر بگیریم. به زبان ریاضی، حد تابع f در نقطۀ c برابر است با L، اگر بهازای هر عدد مثبت مانند ε ، هرقدر کوچک، عدد مثبتی مانند δ وجود داشته باشد، بهقسمی که (فرمول ۴) هرگاه (فرمول ۵)، در اینصورت، مینویسند. (فرمول ۶) و میخوانند «L حد تابع f است، وقتی x به c میل میکند».
فرمول ۴: فرمول ۵: فرمول ۶:
حد تابع وقتی متغیر بینهایت بزرگ میشود، مقداری است که تابع بهاندازۀ دلخواه به آن نزدیک میشود، اگر متغیر را بهاندازۀ کافی بزرگ بگیریم. به زبان ریاضی، حد تابع f وقتی x به سمت بهاضافۀ بینهایت میل میکند برابر L است، اگر بهازای هر عدد مثبت ε ، عددی چون M وجود داشته باشد، به قسمیکه (فرمول ۷) اگر x>M. در اینصورت مینویسند (فرمول ۸). اگر x بهسمت منهای بینهایت میلکند و بینهایت کوچک شود، درتعریف بالا بهجای x>M باید قرار داد x<M و نوشت (فرمول ۹).
فرمول ۷: فرمول ۸: فرمول ۹:
