حساب دیفرانسیل و انتگرال
حساب دیفْرانْسیِل و اَنتِگرال (calculus)
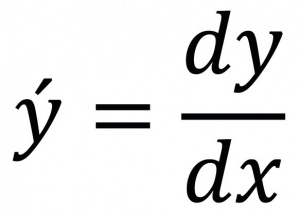
(یا: حسابان) مبحث مهمی در ریاضیات، مرکب از دو شاخۀ حساب دیفرانسیل[۱] و حساب انتگرال[۲]. این مبحث با تکیه بر مفهوم حد[۳] و فرآیند حدی، به بررسی آهنگ تغییر[۴] تابع[۵] نسبت به تغییر متغیر مستقل[۶]، راههای یافتن تابعی با آهنگ تغییر معین، و مفاهیم وابسته و کاربردهای آن میپردازد. حسابان شاید پرکاربردترین بخش ریاضیات باشد. در تحلیل بسیاری از مسائل زندگی واقعی کمیتی را بهشکل تابعی از کمیتی دیگر بیان میکنند، مثلاً موضع یک شیء متحرک را بهصورت تابعی از زمان، دمای یک شیء را بهصورت تابعی از فاصله از منبع گرما، و نیروی وارد بر شیء را بهصورت تابعی از فاصله از منشأ نیرو بیان میکنند. حسابان به بررسی اینگونه توابع و تغییرات آنها میپردازد و ابزار بسیار نیرومندی برای بررسی و محاسبۀ کمیتهایی است که پیوسته تغییر میکنند؛ ازجمله به دانشمندان کمک میکند تا مکان موشکی فضایی را که از زمین دور و دورتر میشود لحظه به لحظه تعیین کنند. آهنگ دقیق یا لحظهای تغییر تابع نسبت به تغییر متغیر با مفهوم مشتق[۷] بیان میشود (← مشتق). اگرy تابعی از متغیر مستقل x و بهصورت y=f(x) باشد، نمو دلخواهی از متغیر x را دیفرانسیل x و حـاصلضرب مشتق تابع y در دیفرانسـیل x را دیفرانسیل تـابع y مینـامند. مشتق تابع را با 'y یا f '(x) و دیفرانسـیل x را با dx و دیفرانسیل y را با dy نمایش میدهند. بنابراین dy = y'dx یا (فرمول ۱) حساب دیفرانسیل به کمک مفاهیم مشتق و دیفرانسیل به بررسی تغییرات توابع و کاربردهای آن میپردازد؛ از آن جمله است مطالعۀ شیب منحنیها، سرعتهای نایکنواخت، شتاب، نیرو، تقریبزدن مقادیر تابع، و تعیین نقاط ماکسیمم و مینیمم.
فرمول ۱:
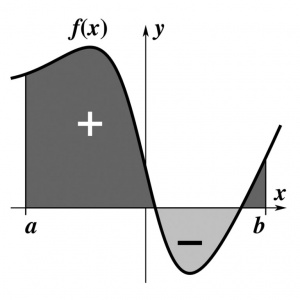
حساب انتگرال با عکس عمل مشتقگیری، یعنی تعیین تابع از روی مشتق یا دیفرانسیل آن (انتگرالگیری)، و کاربردهای متعدد آن سروکار دارد و ازجمله برای محاسبۀ سطح، حجم، و گرانیگاه اجسام، و جوابهای معادلات دیفرانسیل بهکار میرود. ایدۀ اولیۀ حساب انتگرال از مجموع حدّی کمیتهایی نشأت گرفت که تعدادشان زیاد و زیادتر و مقدار هریک کوچک و کوچکتر میشود. در محاسبۀ سطح محدود به یک منحنی، مساحت چنین سطحی را میتوان با تقسیم آن به تعدادی مستطیل با پهنای یکسان و سپس افزایش تعداد مستطیلها و کاهش پهنای آنها برآورد کرد، زیرا هرچه تعداد مستطیلها بیشتر شود، مساحت آنها که با ضربکردن طول در عرض آنها قابل محاسبه است، مجموعاً به سمت سطح زیر منحنی میل میکند. این روش، به روش افناء[۸] معروف است و قدمت زیادی دارد، ولی اهمیت و زیبایی حسابان در این است که روشی اصولی و منظم برای محاسبۀ دقیق بسیاری از مساحتها، حجمها، و سایر کمیتهایی فراهم میکند که یافتن آنها دور از دسترس روشهای باستانی بود. در قرن ۱۷، آیزاک نیوتون[۹] و گوتفرید لایبنیتس[۱۰] برای نخستینبار و مستقل از هم، قواعدی کلی برای حساب دیفرانسیل و انتگرال بنیاد نهادند، هر چند استقرار این موضوع بر پایهای منطقی و مطمئن، عمدتاً بهسبب وجود ابهاماتی در مفاهیم بغرنج حد و پیوستگی، کار دشواری بود. بهجای استفاده از ایدۀ حد، ریاضیدانان قرنهای ۱۸ و ۱۹ حسابان را بر مفهوم «بینهایت کوچکها[۱۱]» و به بیان نادقیق، کمیتهای بسیار کوچک و «دیفرانسیلها» استوار ساختند و به این سبب، این مبحث را «حساب بینهایت کوچکها» خواندند. نخستین شرح کامل حساب دیفرانسیل و انتگرال با استفاده از حد را در ۱۸۲۱، اوگوستین کوشی[۱۲] عرضه کرد، ولی ایدههایش تا سالها بعد، بهخصوص در انگلستان، از اقبال عمومی برخوردار نشد. شاخهها و مباحث ریاضی گوناگونی از حسابان سر برآوردهاند، ازجمله معادلات دیفرانسیلی که شامل مشتقاتی از توابع و احتمالاً خودِ توابعاند. بسیاری از این معادلات مدل ریاضی پدیدههای فیزیکی گوناگونی از قبیل حرکت هماهنگ سادهاند. معادلات دیفرانسیل را عموماً با انتگرالگیری حل میکنند. اگر هیچ روش تحلیلی دیگری در دست نباشد، از روشهای عددی[۱۳] برای انتگرالگیری استفاده میکنند. حساب تغییرات[۱۴] (وردشها) ازجمله دیگر مباحث منشعب از حسابان است. امروز حساب دیفرانسیل و انتگرال را در سطح مقدماتی و پیشرفته، و نیز مباحثی نظیر معادلات دیفرانسیل، و اصولاً همۀ مباحث مطالعۀ تغییرات تابع براساس فرآیند حدگیری را با نام کلی آنالیز[۱۵] میشناسند.
