معادله درجه دوم
معادلۀ درجه دوّم (quadratic equation)
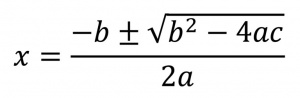
در ریاضیات، معادلهای چندجملهای[۱] که بزرگترین توان[۲] مجهول آن ۲ است. صورت کلی این معادله، ax۲ + bx + c = ۰ است که در آن، b، a، و c عددهایی حقیقی[۳]اند و ضریب[۴] a صفر نیست. در هندسۀ تحلیلی[۵]، تابع درجۀ دوم[۶]، یعنی تابعی بهصورت y = ax۲ + bx + c، معرف سهمی[۷] است. بعضی از معادلات درجۀ دوم را با تجزیۀ معادله به عوامل[۸] آن حل میکنند. مثلاً برای حل معادلۀ x۲ - ۱ = ۰ ، ميتوان نوشت (x - ۱)(x + ۱) = ۰ و درنتیجه، x = ۱ و x=-۱ . در حالت کلی، جوابها یا ریشههای معادلۀ درجه دوم از (فرمول ۱) بهدست میآیند.
فرمول ۱:
عبارت b۲ - ۴ac را مبین[۹] مینامند. اگر مبین مثبت باشد، معادلۀ درجۀ دوم دو ریشۀ حقیقی متمایز[۱۰] دارد؛ اگر صفر باشد، معادله دو ریشۀ حقیقی برابر، معروف به ریشۀ مضاعف[۱۱] یا دوگانه؛ و اگر منفی باشد، معادله دو ریشۀ مختلط متمایز[۱۲] دارد.
