لگاریتم
لُگاریتم (logarithm)
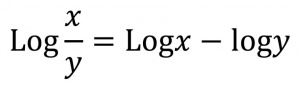
نمای نشاندهندۀ عدد در پایه[۱]ای معیّن. پایۀ لگاریتم متعارفی ۱۰ است. مثلاً لگاریتم ۱۰۰۰ در پایۀ ۱۰ برابر ۳ است، زیرا ۱۰ باید به توان ۳ برسد تا ۱۰۰۰ بهدست آید. لگاریتم [۲] در این پایه ۰.۳۰۱۰ است، زیرا ۳۰۱۰/۰ ۱۰=۲. جزء صحیح۲ لگاریتم را مفسّر[۳] و جزء کسری اعشاری[۴] آن را مانتیس[۵]میگویند. پیش از عرضۀ حسابگرهای الکترونیک ارزانقیمت، بهمنظور سادهسازی محاسبات، بهجای ضرب و تقسیم اعداد، لگاریتمهای آنها را جمع و تفریق میکردند، زیرا طبق قواعد لگاریتم، Log (xy) = Log x + Log y و (فرمول ۱) پس میتوان لگاریتمهای x و y را جمع کرد و سپس آنتیلگاریتم[۶] جواب، یعنی عددی را که لگاریتم آن برابر جواب است، از جدول یافت.
فرمول ۱:
جدولهایی برای لگاریتم و آنتیلگاریتم در دستاند که تبدیل اعداد به لگاریتمها و بالعکس را نشان میدهند. مثلاً برای ضربکردن ۶۵۶۰ در ۹۸۰، لگاریتمهای آنها، ۳.۸۱۶۹ و ۲.۹۹۱۲، را از جدول مییابیم و با هم جمع میکنیم. حاصل ۶.۸۰۸۱ است. سپس، آنتیلگاریتم این عدد را که برابر با ۶,۴۲۸,۸۰۰ است مییابیم. پایۀ لگاریتم طبیعی[۷] یا نپری[۸]، عدد e، عددی گنگ[۹] و تقریباً برابر با ۲.۷۱۸۳ است. اصل لگاریتم مبنای تهیۀ خطکش محاسبه بود. با رواج گستردۀ حسابگرهای الکترونیک جیبی، نیاز به لگاریتم کاهش یافت. نخستین جدول لگاریتم[۱۰] در پایۀ e را ریاضیدان اسکاتلندی، جان نپِر[۱۱]، در ۱۶۱۴ منتشر کرد. لگاریتمهای در پایۀ ۱۰ را هنری بریگز[۱۲] انگلیسی (۱۵۶۱ـ۱۶۳۱) و آدریان ولاک[۱۳] هلندی (۱۶۰۰ـ۱۶۶۷) عرضه کردند.
